The era of a non-classical probability

The idea that the probabilities governing quantum phenomena were different from classical, was present from the very beginning of the theory. Later, research revealed that quantum states could be considered as a very peculiar form of non-commutative probability calculus. Since then, different ways of describing quantum states were discovered, including measures over orthomodular lattices and negative probabilities as well. The idea that some problems can be dealt more naturally using probabilities that depart from classical have inspired a research field that goes far beyond quantum physics.

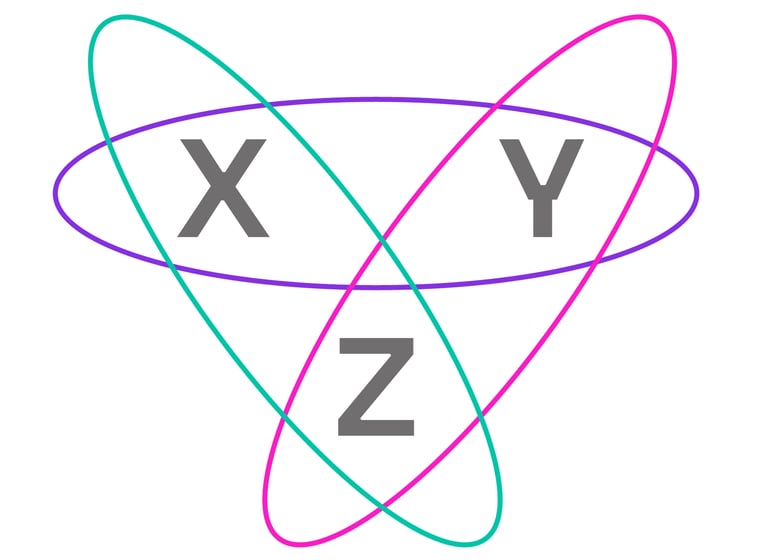
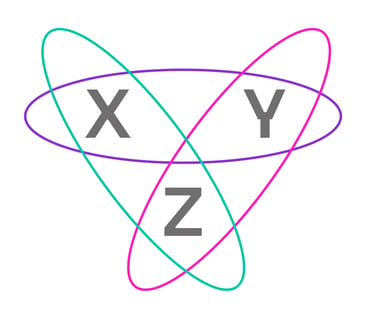
Our research

We study different ways of characterizing quantum states as non-Kolmogorovian probability measures. These include the standard description based in the orthomodular lattice of projection operators associated to a separable Hilbert space, and the negative probabilities approach. Furthermore, by describing quantum states in terms of measure theory, one obtains a powerful formal framework for distinguishing between classical and quantum physics, and characterizing the most salient quantum features. If a decision agent deals with events that can be endowed with a Boolean algebra structure, then, the most rational choise is Kolmogorov's axioms. We have proved that if the events are organized in terms of incompatible contexts (as in quantum physics), quantum-like probabilities arise in a very natural way. Naturally, we also do research in quantum tomograpic and quantum state estimation techniques.

Our goals

The challenge of explaining the peculiar rules that govern quantum probabilities is one of the main goals in the field of the foundations of physics. We seek to answer the question: What are the axioms that singularize quantum physics among a vast family of no-signal theories? More specifically, we aim to gain knowledge about how quantum contexts intertwine each other giving place to Hilbert space quantum mechanics. Another critical aspect of quantum physics is that randomness seems to have a non-reducible nature in the quantum realm. The idea of a non-deterministic world combined with the rules of a non-Kolmogorovian probability calculus needs to be understood in connection with the development of quantum technologies and the problem of understanding quantum advantage.

Our team

Our strength lies in our individuality. Set up by Esther Bryce, the team strives to bring in the best talent in various fields, from architecture to interior design and sales.