Context is everything
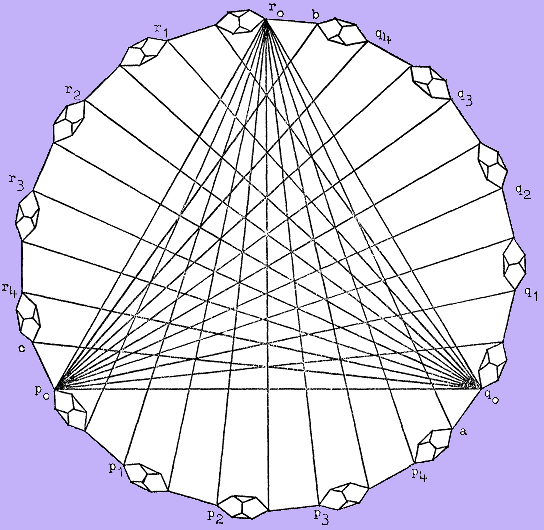
Every quantum phenomenon occurs in relation to a particular measurement context. This was emphasized by N. Bohr since the very beginnings of the theory. One of the rules of standard quantum theory is that "unperformed experiments have no results", meaning that one should not use counterfactual reasoning combining the results of incompatible experiments if one wants to avoid contradictions. In a related way, standard quantum physics dictates that one should not assign observed results to properties of the systems before measurement. In 1967, S. Kochen and E. Specker proved a major theorem in the history of quantum foundations and quantum logic. Roughly speaking, the theorem says: it is not possible to assign values to all possible quantum observables in a context-independent way. Their goal was to rule out a certain family of hidden-variable theories. Since then, the notion of quantum contextuality became a main topic in the foundations of quantum physics, now believed to have implications for understanding quantum advantage.
Our research
Contextuality is deeply related to the non-existence of a joint (classical) probability out of which the probabilities associated to the different measurement contexts can be computed as marginals. There are different ways to deal with this problem. We have approached it in connection to quantum indistinguishability. More generally, we have explored the idea that the notions of contextuality and indistinguishability are deeply connected in quantum physics. Following that approach, it is possible to motivate a connection between indistinguishability and negative probabilities that gives plays to a contextuality measure that can be used to quantify quantumness.
Our goals
Our goal is to explore new ways of understanding the role of quantum contextuality in the foundations of quantum physics, especially, in connection to quantum indistinguishability. In particular, to gain a deeper understanding of how contexts are intertwined, and how this is so in quantum theory (in contrast to other possible no-signal theories). Also, we look for theoretical tools allowing us to quantify contextuality in problems related to quantum technolgies. During the last years, many studies pointed out that the quantum advantage might be related to contextuality. We are currently working in characterizing how contextuality, understood as a resource, is distributed in quantum random circuits for different sets of elementary quantum gates.