Quantum and beyond
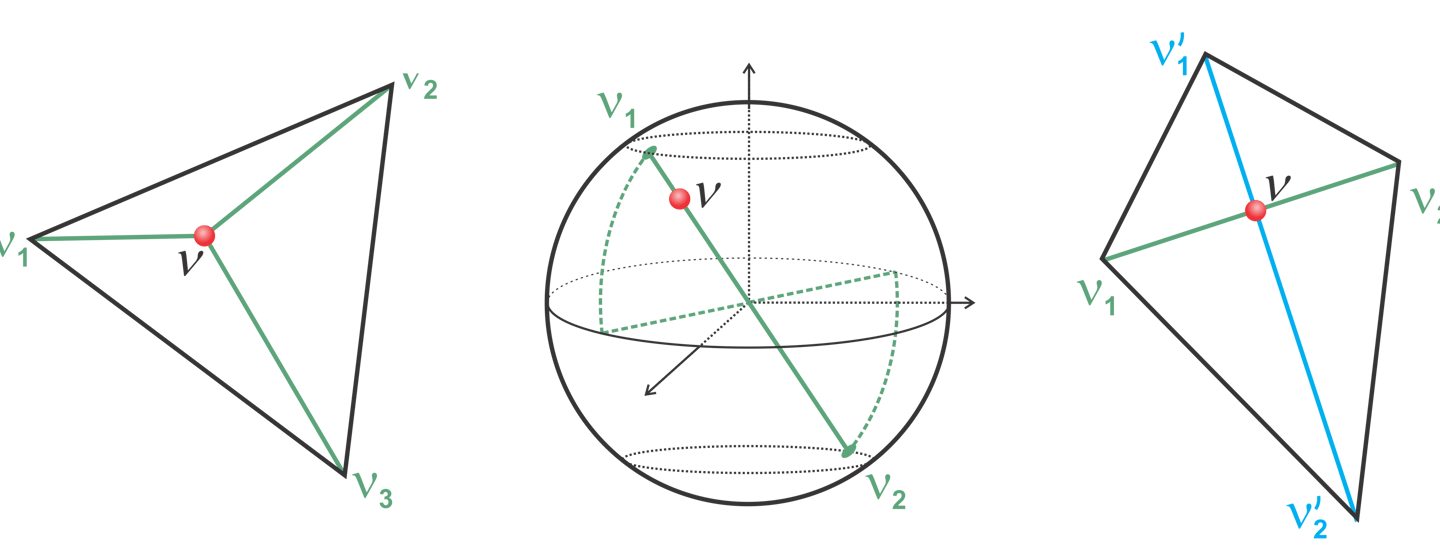
Quantum theory shows us a very peculiar probability calculus. This implies that when we study correlations between different parties, they must obey the probabilistic rules of quantum physics. This entails that, for example, in the CHSH inequality, a singlet state will reach a particular value of violation. Why nature choses quantum theory among all conceivable no-signal theories? This is one of the major questions in the foundations of physics nowadays: what axioms should we impose on the probabilities of a theory in order to obtain quantum theory? Gleason's theorem implies that quantum states can be formulated as measures over orthomodular lattices. More specifically, lattices that are isomorphic to the closed subspaces of a separable Hilbert space. But lattice theory gives place to lattices that are very different from those originated in quantum models. There exists more general structures, such as sigma-orthomodular postes and automaton logics. These mathematical frameworks allow us to conceive theories which, besides being compatible with special relativity, are very different from quantum theory. Therefore, it can be used as a natural background for exploring theories beyond quantum physics and, at the same time, try to discover the axioms that singularize quantum theory out of a plethora of posibilities.

Our research
We have studied different forms of generalized probability theories. In particular, we have suggested that quantum information theory can be considered as a non-Kolmogorovian version of Shannon's theory. This idea can be extended to quantum computing, by using the general probabilistic models approach.
Our goals
By using the approach based in generalized probabilistic models we seek to understand better the differences between classical and quantum physics, and classical and quantum information and computing. In particular, we look for the implications that these differences have with regard to the problem of deriving quantum theory from simple general axioms.